Technical Analysis

Overview

In order for any designs to be put into action, a series of technical analyses must be performed to ensure all equipment is safe and capable of performing the required tasks. A large focus was initially placed on determining the vertical force present at the plate. Knowing the vertical force it must withstand allows for a better understanding of the different component requirements. Some initial assumptions taken into account are listed below. These assumptions are used to aid the analyses described in the following sections.

Initial Assumptions:

Test will exist at vacuum conditions (low pressure environment)
Primary jet flow will be bounded by the apparent shock
Flow expands isentropically in test section
Flow bounded entirely by apparent jet shock
Flow stagnates completely in the impinging zone
Specific heat ratio is independent of temperature
Reservoir is very large

Diagram of general flow behavior.

Knudsen Number

The Knudsen number is dimensionless number defined as a ratio of the mean free path over the characteristic length of the system. Low Knudsen numbers are associated with denser gasses, while higher Knudsen numbers are associated with more rarefied gasses. The Knudsen number is an important calculation because it provides insight to the validity of the continuum assumption of a fluid field. If the Knudsen number is greater than 0.1, then the fluid system can no longer be treated as a continuous mass, and instead must be considered from the perspective of individual gaseous particles. Not only will the presence of a higher Knudsen number invalidate the use of prominent equations such as the Navier-Stokes equation, but it will also likely result in different pressure readings on the plate.

Simplified Knudsen Number equation.

Equations to solve for Knudsen Number.

Reynolds Number

The Reynolds number is dimensionless number defined as a ratio between the inertial and viscous forces present in a fluid flow. This number is important for maintaining dynamic similarity in scaled down flows. By creating flows of similar Reynold’s numbers, it can be ensured that the fluid interactions present in both flows will be similar.

Equation to solve for Reynolds Number.

Isentropic Expansion (Speed Relations)

As a supersonic, compressible gas expands in a vacuum, it will increase its speed in order to preserve a constant mass-flow rate. As a result, the speed of the gas leaving the nozzle will not be the same as the speed of the gas before contact on the plate. Analyzing the images of prior experiments and conservatively assuming the geometry of the flow to be bounded by the geometry of the initial shock, the isentropic expansion formula shown can be used to determine the speed of the gas, as a function of Mach number, before contact on the plate. While the equation shown is often used in the context of constructing rocket nozzles, it is equally applicable to this case. The listed equation defines the ratio of the exit area to the throat area as a function of Mach number and the specific heat ratio. However, if the geometry of the flow is pre-defined, as is the case here, the area ratio and specific heat ratio can be used to determine the speed of the flow.

Equation relating exit and throat areas as function of Mach number and specific heat ratio.

In order to use this equation, the areas must be known. Using images taken from previous tests, it was determined that the area values can be found in MATLAB by counting the pixels as shown in the following images. This pixel measurement can then be converted into usable units by scaling the pixel to length ratio.

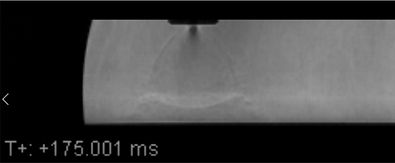
Test of past apparatus with steady developed flow (h/D = 10, P = 5.3 Torr).

Test of past apparatus after pixel counting through MATLAB.

Shock Pressure Losses

Shock waves are highly entropic phenomena. The abrupt changes in gas properties over the propagation of a normal shock wave causes massive amounts of energy, that would normally express itself in the form of pressure, to be converted to entropy. As a simplification, the reservoir stagnation pressure will be assumed equivalent to its static pressure. The given equation therefore relates the static pressure of the reservoir to the stagnation pressure present on the plate. This will provide insight to the expected forces on the plate during the test. This equation also establishes a direct relationship between the reservoir pressure and the stagnation pressure on the plate.

Normal shock relation between Mach number and stagnation pressure.

MATLAB Calculator

In order to simplify the technical analysis process, a MATLAB script was created. This script includes all the basic equations detailed above for the purpose of calculating the properties of the fluid flow right before hitting the plate. The values found through this calculator were verified against values found using the Virginia Tech Online Compressible Aerodynamics Calculator, a tool publicly available and displayed below.

MATLAB Script Example.

VA Tech Online Compressible Aerodynamics Calculator Example.

After validation of the MATLAB calculator, the expected force on the plate was determined to be roughly 50N. Additionally, the expected pressure was determined to be roughly 174Pa.